A proporção áurea vem encantando pessoas ao longo de séculos. Dizem que ela pode ser encontrada na natureza, na arquitetura, em pinturas de Leonardo da Vinci e até no corpo humano. Infelizmente, boa parte do mito que rodeia a divina proporção foi bastante exagerado.
Alguns estudiosos – como o matemático Keith Devlin, o físico Donald E. Simanek e o astrofísico Mario Livio – vêm tentando por muitos anos desmistificar a proporção áurea. Por exemplo, Devlin nota que diversos exemplos populares – o Partenon, as pirâmides egípcias, a Mona Lisa – na verdade não se encaixam na proporção áurea. O que há de real na divina proporção? Vamos conferir.
Um pouco de história
Antes de tudo: o que é a proporção áurea? Ela surge quando você divide uma linha em dois pedaços (A e B), de forma que a razão entre eles (A/B) é igual à razão entre a linha inteira e o pedaço maior ((A+B)/A). Isto é aproximadamente igual a 1,618.
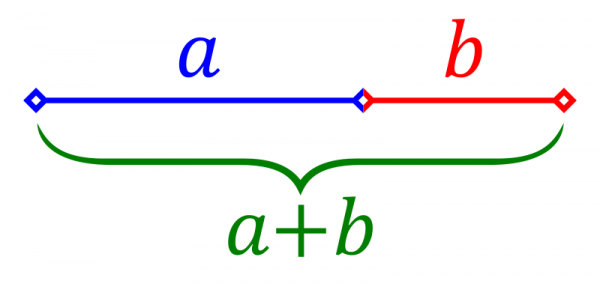Stannered/Wikipedia
Ela é representada pela letra grega phi (φ), e foi descoberta pelo matemático Euclides há 2.300 anos, na Grécia Antiga – mas só ganhou o nome “divina proporção” muitos séculos depois.
Na verdade, esse nome surgiu a partir de uma confusão: em 1509, Luca Pacioli escreveu o livro De Divina Proportione, no qual ele analisava essa proporção. Pacioli não acreditava que ela deveria ser aplicada à arte nem à arquitetura: em vez disso, ele defendia o sistema vitruviano de proporções racionais.
Mas, em 1799, começaram a dizer que Pacioli havia criado uma teoria da estética baseada na proporção áurea. Para aumentar a confusão, o livro foi ilustrado por seu amigo, Leonardo da Vinci. Daí a dizer que da Vinci usou a tal proporção em suas pinturas, como a Mona Lisa, foi um pulo.
O número ganhou ainda mais popularidade por causa de Adolf Zeising, um psicólogo alemão que via a razão áurea em “todas as estruturas, formas e proporções”. Ele dizia que a distância entre o umbigo e os pés sempre se encaixa na proporção áurea – ou seja, seria muito próximo a 1,6.
As teorias de Zeising se tornaram terrivelmente populares no século XIX, e repercutem até hoje – mesmo não estando certas. O matemático Keith Devlin diz à Fast Company: “ao medir algo tão complexo como o corpo humano, é fácil chegar a exemplos de razões que chegam muito perto de 1,6″.
Claro, nem tudo sobre a proporção áurea é “uma lenda urbana, um mito”, como diz erroneamente a Fast Company. Vamos separar o joio do trigo, e ver onde a proporção áurea realmente se aplica – e onde usá-la é forçar a barra.
Onde existe a proporção áurea
A proporção áurea não é uma “mentira”. Ela aparece bastante na ciência e na natureza, em diferentes formas.
Uma delas é a espiral áurea, que cresce de acordo com a razão φ. É possível se aproximar dela dividindo-se os lados de um retângulo em proporções áureas e ligando os pontos com um compasso.
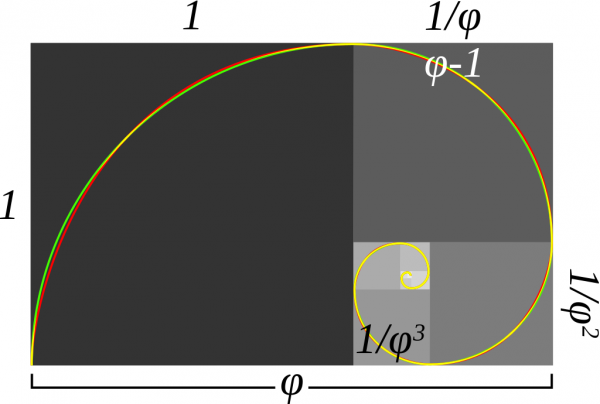
A linha vermelha é a espiral áurea; a linha verde é a aproximação feita com quartos de cirncunferência; a linha amarela é a sobreposição entre as duas. (Wikipedia)
Ela também está relacionada à importante sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Ela é formada pela soma dos dois números anteriores: 1+1=2, 1+2=3, 2+3=5, e assim por diante. Ao dividir um número pelo outro, você se aproxima continuamente da proporção áurea.
É possível encontrar exemplos da espiral áurea e da sequência de Fibonacci na natureza.Como explica a revista Nautilus:
Por exemplo, indícios da proporção áurea foram detectados no nível quântico, onde átomos magnéticos ligados entre si parecem vibrar em frequências descritas por φ. Na escala macroscópica, a sequência de Fibonacci e a proporção áurea descrevem as disposições naturais de sementes e folhas em muitas plantas. Se você examinar a embalagem de sementes na cabeça de um girassol, há uma série de espirais no sentido horário e anti-horário, que geralmente aparecem em números de Fibonacci sucessivos.
Institute of Science in Society via CNET
O matemático Revlin explica que, no caso do girassol, “a natureza quer colocar o máximo de sementes possível, e a maneira de fazer isso é adicionar novas sementes numa forma em espiral”. Vale notar que girassóis nem sempre obedecem à sequência de Fibonacci.
Revlin também nota que a razão áurea também está relacionada ao pentagrama (estrela de cinco pontas), a certas estruturas cristalinas e a fractais.
A proporção áurea também era usada como um guia na obra de artistas como Salvador Dalí e de arquitetos como Le Corbusier.
A Última Ceia (1955), por Salvador Dalí, com linhas inseridas pelo programa PhiMatrix
Onde não existe a proporção áurea
A proporção áurea não está presente em todos os lugares da natureza, nem da arte. No entanto, é muito fácil enxergar padrões onde eles não existem. Revlin explica:
A questão aqui não é se você pode encontrar a proporção áurea em algum lugar. Se você olhar o bastante, você será capaz de encontrar qualquer número (razoável) em quase qualquer lugar…
Faça a pergunta: existe uma boa explicação científica para mostrar por que a razão áurea aparece? Há provas definitivas de que, por exemplo, um determinado artista fez uso deliberado da proporção áurea em seu trabalho? Se não, tudo que você tem é uma crença sem fundamento.
Obras históricas
Há quem diga que a fachada do Partenon, templo construído na Grécia Antiga para louvar a deusa Atena, foi feito com base na proporção áurea. No entanto, ele foi construído em 447 a.C., mais de um século antes que Euclides descobrisse a razão áurea. Como o arquiteto Fídias usaria esse número sem conhecê-lo?
Além disso, as medidas da fachada não se encaixam na proporção áurea. Isso só funciona quando você “força a barra” e inclui no retângulo parte dos degraus:
Original por Sébastien Bertrand/Flickr
Isso é totalmente arbitrário. Claro que, se você tentar encaixar uma espiral áurea apenas na fachada, ela não vai caber:
Também existe a crença de que Leonardo da Vinci usou a proporção áurea em suas obras. Por exemplo, dizem que o Homem Vitruviano se encaixa na razão áurea, por ter a proporção perfeita entre altura e largura – mas as medidas não batem. Como explica o físico Donald E. Simanek:
A relação umbigo/altura na imagem é 0,604, um pouco menor do que 1/φ = 0,618. Da Vinci escreveu um texto que acompanha a imagem, mas ele não diz nada sobre essa relação, nem sobre a distância do umbigo até os pés. O texto não contém nenhuma menção de φ. Não há nenhuma sugestão na imagem de que Leonardo estava fazendo algo mais profundo do que relacionar o homem a um círculo e um quadrado.
Na verdade, parece que Leonardo forçou as proporções do homem para se encaixar nessas figuras geométricas. Se Leonardo quisesse incorporar φ na imagem, ele poderia facilmente ter movido um pouco a posição do umbigo. O fato de que ele não fez isso nos diz que ele não tinha qualquer razão para fazer isso.
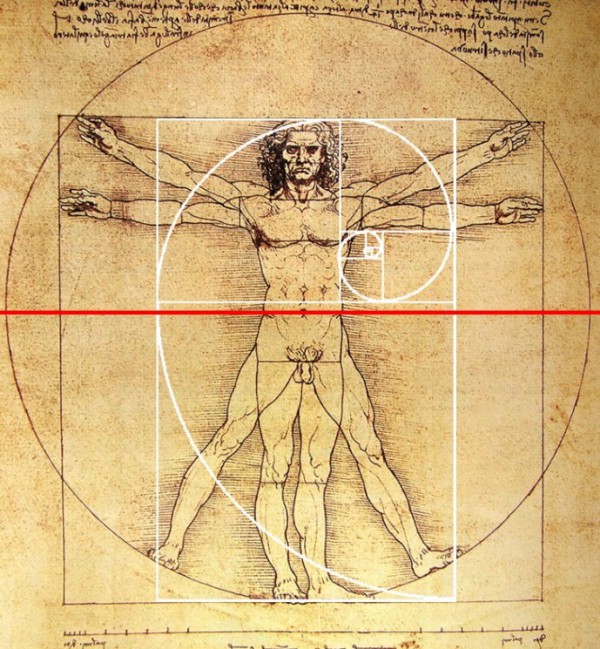O retângulo áureo e a linha do umbigo. Eles não se encaixam.
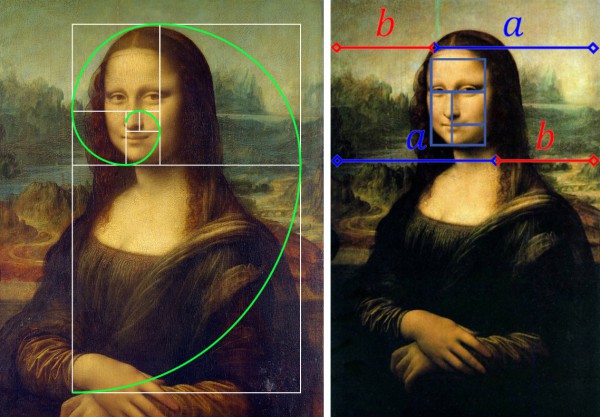
A Mona Lisa também é “vítima” das linhas áureas. Basicamente, você pode inserir um retângulo áureo arbitrário na cara da Gioconda, e ele vai se encaixar… de alguma forma. Eis alguns exemplos:
Pencil Scoop/Photoshop Tutorials
Na primeira imagem, a espiral áurea começa, sem motivo, do espaço entre as mãos da Mona Lisa. Na segunda imagem, colocaram um retângulo começando na testa da mulher, só para ele ficar alinhado com os olhos e o lábio superior. Vale tudo! Nesse espírito, eis minha contribuição:
Até mesmo Mario Livio, autor do livro que é referência na história do φ, jogou a toalha: “isso tem sido alvo de tanta especulação erudita e popular que fica praticamente impossível chegar a quaisquer conclusões inequívocas”.
Padrão de beleza
Ei, mas a razão áurea não era uma “proporção da beleza universal”? Bem, um estudo de 2009 fez quatro experimentos para testar a existência de um arranjo facial que fosse considerado bonito pela maioria das pessoas. Os cientistas descobriram que as proporções não se encaixam na razão áurea:
Faces femininas foram julgadas mais atraentes quando a distância vertical entre os olhos e a boca era aproximadamente 36% do comprimento do rosto, e a distância horizontal entre os olhos era de aproximadamente 46% da largura do rosto.
Mas se você está determinado a ver proporções áureas, você vai encontrá-las. Esta é uma imagem do site GoldenNumber.net:
Os retângulos não se encaixam muito bem nos cantos dos olhos, nem nos cantos da boca, e outros mal fazem sentido (o que o primeiro retângulo azul está medindo, exatamente?). Só que isso é o bastante para fazer muitas pessoas acreditarem na conexão entre proporção áurea e beleza.
A razão áurea foi usada até mesmo para criar a “máscara Phi“, um modelo patenteado de beleza para rostos femininos criado pelo cirurgião plástico Stephen Marquardt:
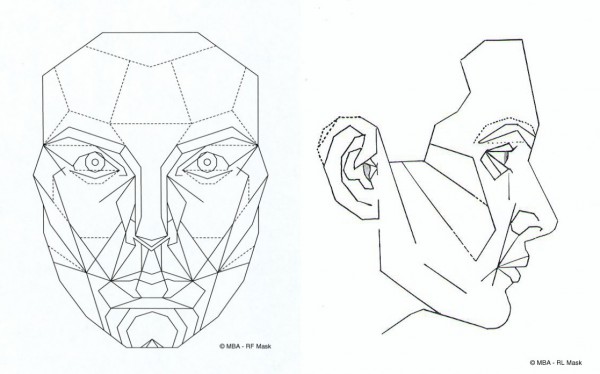
Essa ideia é refutada por um estudo de 2008, que diz: “as alegações de Marquardt sobre sua máscara não são consistentes com a literatura existente sobre correlatos de beleza facial”. Na imagem abaixo, o rosto “recomendado” pela máscara Phi está à esquerda; ele é realmente mais bonito que o rosto à direita?
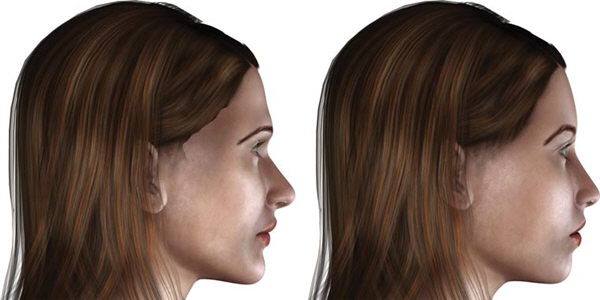
O designer russo Igor K-Chm fez uma brincadeira sobre o assunto em “Cirurgia Plástica do Dr. Fibonazi“:
Na natureza
Outro exemplo – desta vez menos polêmico – é a concha do náutilo, um molusco que vive no Oceano Pacífico. Ela tem formato de espiral, mas não obedece nem de longe a proporção áurea:
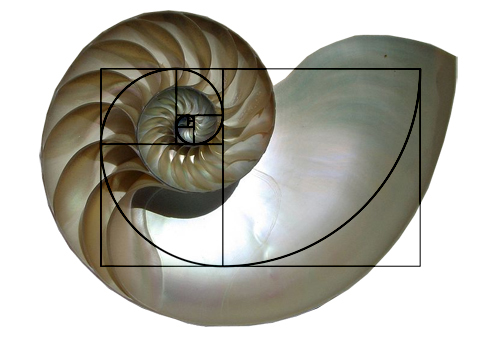Chris 73/Wikipedia modificada por Photoshop Tutorials
Esse formato corresponde ao de uma espiral logarítmica, que permite à concha crescer sem mudar de forma. Para fazer isso, ela não precisa obedecer a razão áurea.
Também é possível encontrar espirais logarítmicas em galáxias, só que elas geralmente não se encaixam na proporção áurea:
Pencil Scoop
Até na Apple?!
Tentaram até relacionar a espiral áurea com o logotipo da Apple (socorro). O designer brasileiro Thiago Barcelos elaborou a imagem abaixo, que parece mostrar como a sequência de Fibonacci se encaixa na maçã:
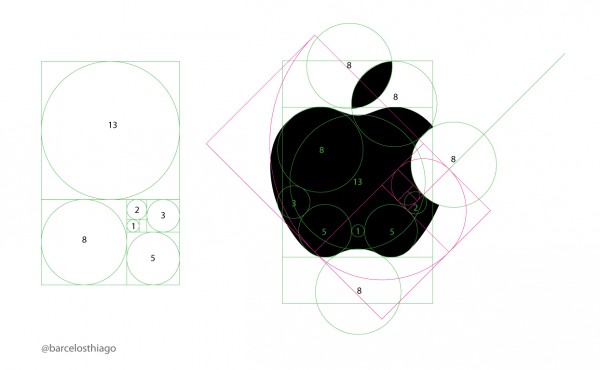
Só que essa não é a maçã real da Apple. O logotipo de verdade não se encaixa numa espiral áurea:
O Thiago também criou essa imagem, dando a entender que o iPhone 4 obedece a proporção áurea:
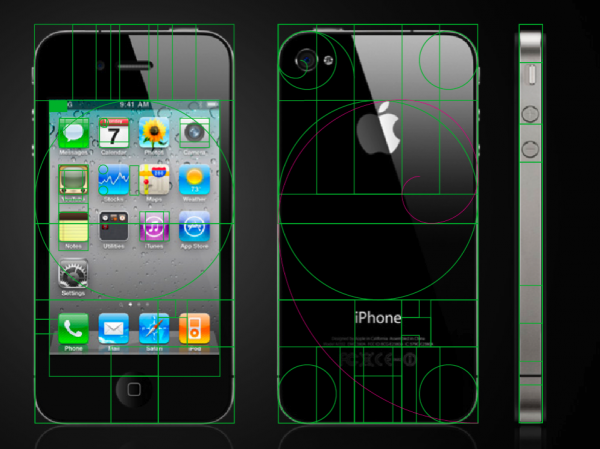
Mas David Cole, diretor de design no Quora, diz que um iPhone com proporções áureasseria mais ou menos assim:
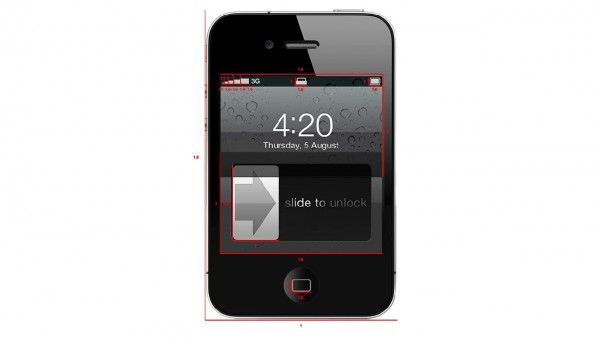
Nós poderíamos listar inúmeros outros exemplos: moléculas de DNA, furacões, padrões de voo de animais etc. Sempre vão tentar encaixar algo na proporção áurea – na maioria dos casos, será algo equivocado.
Por que vemos a proporção áurea onde ela não existe
Montagem bem-humorada que circula na internet há alguns anos; esta não é uma espiral áurea.
A razão áurea pode ser, sim, encontrada na natureza e na arte. No entanto, há quem faça um esforço tremendo para visualizá-la onde ela não existe. E talvez essas pessoas nem acreditem que a divina proporção é menos comum do que elas imaginam!
Por que isso acontece? O matemático George Markowsky, em seu artigo “Equívocos sobre a Razão Áurea” de 1992, explica:
Se você se dispõe a medir uma estrutura complicada como uma pirâmide egípcia, você terá rapidamente na mão uma grande abundância de comprimentos para brincar. Se você tiver paciência suficiente para fazer malabarismos com esses números, você certamente obterá muitos valores que coincidem com importantes datas históricas ou números nas ciências. Como você não está limitado por nenhuma regra, seria estranho se a “verdade” da razão áurea não se encaixasse com sucesso considerável.
Ou seja, quando você se dispõe a analisar algo complexo – como o rosto humano, ou enormes obras de arquitetura – é muito fácil encontrar medidas e proporções que se encaixem com algo que você procura, como a razão áurea.
E por que as pessoas fazem isso? Há um motivo mais profundo, como explica a revista Nautilus:
Basicamente, quanto mais fácil for o entendimento de uma situação (por ser matematicamente simples, por termos visto muitas vezes antes, por ser simétrico, etc.), mais provável é que pareça certo… E talvez, como a razão áurea tem se revelado interessante em certos aspectos, e é fácil de entender, as pessoas saltam naturalmente à conclusão de que ela também deve ser usada em outros casos nos quais a proporção simplesmente não é encontrada.
É muito gratificante descrever a natureza através de simetrias, razões e medidas unificadas. Isso nos dá uma sensação de controle, e faz parecer que o mundo à nossa volta pode ser melhor compreendido.
Infelizmente, isso nem sempre é verdade, mesmo que nossa mente esteja determinada a encontrar padrões onde eles não existem. No fim, é uma diferença entre matemática e numerologia: algo que parece impressionante à primeira vista, mas que desmorona sob um olhar mais atento.
Nem tudo que reluz é ouro – nem mesmo a proporção áurea.
Foto inicial por Prab Bhatia/Flickr
Fonte: Gizmodo Brasil
